"Euler #7 : Benchmarked Primes"

by Nicolas Wu

Posted on 12 August 2010

Tags: Haskell, Euler

This week’s Project Euler question is:

Find the 10001st prime.

We already described a simple algorithm for finding primes in a previous post, so rather than repeat ourselves, in this article we’ll discuss benchmarking using Criterion to find the fastest prime number algorithm that doesn’t require too much magic. I’ll be taking implementations found on the Haskell wiki.

Imported modules

First we’ll need to import the Criterion modules, which provides us with our benchmarking suite:

> import System.Environment (getArgs, withArgs)
> import Criterion (bgroup, bench, nf)
> import Progression.Main (defaultMain)
> import Data.List.Ordered (minus, union)

I’ll actually be using Progression in conjuction with Criterion, which just makes collecting the results of several benchmarks a little easier.

Prime Algorithms

The prime number generator we used previously was Turner’s sieve, defined as follows:

> turner :: [Int]
> turner =  sieve [2 .. ]
>   where
>     sieve (p:xs) = p : sieve [x | x <- xs, x `mod` p /= 0]

The Haskell wiki documents a whole range of other algorithms that can be used to generate primes. Here are the definitions that I pulled from the wiki:

> postSieve :: [Int]
> postSieve = 2 : 3 : sieve (tail postSieve) [5,7..]
>   where
>     sieve (p:ps) xs = h ++ sieve ps [x | x <- t, x `rem` p /= 0]
>                      where (h,~(_:t)) = span (< p*p) xs
> 
> trialOdds :: [Int]
> trialOdds = 2 : 3 : filter isPrime [5,7..]
>  where
>   isPrime n   = all (notDivs n) 
>                   $ takeWhile (\p-> p*p <= n) (tail trialOdds)
>   notDivs n p = n `mod` p /= 0
> 
> nestedFilters :: [Int]
> nestedFilters = 2 : 3 : sieve [] (tail nestedFilters) 5
>  where
>   notDivsBy d n     = n `mod` d /= 0
>   sieve ds (p:ps) x = foldr (filter . notDivsBy) [x,x+2..p*p-2] ds
>                       ++ sieve (p:ds) ps (p*p+2)
> 
> spansPrimes :: [Int]
> spansPrimes = 2 : 3 : sieve 0 (tail spansPrimes) 5
>   where
>     sieve k (p:ps) x = [n | n <- [x,x+2..p*p-2], and [n`rem`p/=0 | p <- fs]]
>                        ++ sieve (k+1) ps (p*p+2)
>        where fs = take k (tail spansPrimes)
> 
> bird :: [Int]
> bird = 2 : primes'
>  where
>   primes' = [3] ++ [5,7..] `minus` foldr union' [] mults
>   mults   = map (\p -> let q=p*p in (q,tail [q,q+2*p..])) $ primes'
>   union' (q,qs) xs = q : union qs xs
> 
> wheel :: [Int]
> wheel = 2:3:primes'
>   where
>     1:p:candidates = [6*k+r | k <- [0..], r <- [1,5]]
>     primes'        = p : filter isPrime candidates
>     isPrime n      = all (not . divides n)
>                        $ takeWhile (\p -> p*p <= n) primes'
>     divides n p    = n `mod` p == 0

I won’t go into the details of explaining these different algorithms, since I want us to focus on how we might benchmark these implementations.

Benchmarking

In order to compare these different algorithms, we construct a program that takes as its argument the name of the function that should be used to produce prime numbers. Once the user has provided this input, the benchmark is executed using Criterion to produce the first 101, 1001, and 10001 primes.

> main = do
>   args <- getArgs
>   let !primes = case head args of
>                  "turner"        -> turner
>                  "postSieve"     -> postSieve
>                  "trialOdds"     -> trialOdds
>                  "nestedFilters" -> nestedFilters
>                  "spansPrimes"   -> spansPrimes
>                  "bird"          -> bird
>                  "wheel"         -> wheel
>                  _               -> error "prime function unkown!"
>   withArgs (("-n" ++ (head args)) : tail args) $ do
>     defaultMain . bgroup "Primes" $
>       [ bench "101" $ nf (\n -> primes !! n) 101
>       , bench "1001" $ nf (\n -> primes !! n) 1001
>       , bench "10001" $ nf (\n -> primes !! n) 10001
>       ]

We then run this code with each prime function name as an argument individually, and the Progression library puts the results together. Here’s a bar chart generated from the data:

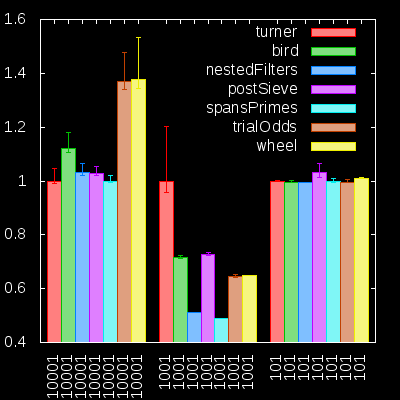
Normalised prime function benchmarks

Normalised prime function benchmarks

These results have been normalised against the turner function, and show the results of how long it took for the various algorithms to find the 10001th, 1001th and 100th primes.

Solving this week’s problem is a simple case of running any one of these algorithms on our magic number:

> euler7 = spansPrimes 10001

Summary

Collecting benchmark information with Criterion and Progression is really quite simple! The best thing about Criterion is that the benchmarking is very robust: detailed statistics are returned regarding the benchmarking process, and whether the results are likely to be accurate. Progression makes the collation of several runs of benchmarks very simple, and means that different versions of a program can be compared with ease.

Comments